Kinetic installation. Acrylic tubes, balls, LEDs, motors and custom software.
Pentavlos is a kinetic light and sound sculpture, where harmony and periodicity are the fundamental elements. Motion, sound and light, all are obeying the laws of the harmonic oscillation.
Five white balls are oscillating inside acrylic tubes using the thrust of small propellers at the bottom of each system. Both balls and the tubes are emitting a light pulse and sound tone in significant point of the movement. Each tube is “tuned” in a different note of a natural pentatonic scale. The periods of the oscillations are accurately adjusted to form visual traveling waves, standing waves and quasi chaos.
There are three chapters:
• City Memories • City Machines • City Lights
![]()
Pentavlos is using a simple mechanism to detect the presence of visitors around it. When there are no visitors, the installation enters a standby mode where it consumes minimum energy.
- Video demonstration of Pentavlos
- Photos of Pentavlos
- Pentavlos and Invisible Cities
- The Theory Behind Pentavlos
- The Sound of Pentavlos
- The Technology of Pentavlos
Festivals & Exhibitions:
Photos of Pentavlos
 |
Pentavlos and Invisible Cities
Pentavlos was presented at Italian Cultural Institution at Athens during a two day even organized by Athens University dedicated to Italo Calvino and his work “Invisible Cities”.
The periodicity and the harmonic motion, which are the key elements of the installation Pentavlos, can also be found in the novel “Invisible Cities” by Calvino. The book is divided into 9 parts, with each part containing a different number of cities. Both the length of the title of each section and how they move from one thematic group to another, follow the rules of the harmonic (sinusoidal) motion. Calvino has also chosen to integrate the periodicity to the repeated structure and the continuous alternation between dialogue and descriptions of cities.

The Theory Behind Pentavlos
Harmonic motion, a periodic movement between two points, occur widely in nature. A simple harmonic oscillator is used to model and explain many phenomena in both classical physics and quantum mechanics from modeling phonons to describing quantum fields. Beyond that, a vast amount of motions, sounds, and systems in general are analyzable as superposition of simple harmonic motions of varying frequencies and amplitudes (Fourier analysis).
If we chose five different harmonic oscillators with gradually different periods, they will start together and quickly will fall out of sync, because of their different periods of oscillation, and soon they start to form visual traveling waves, standing waves and quasi chaos.
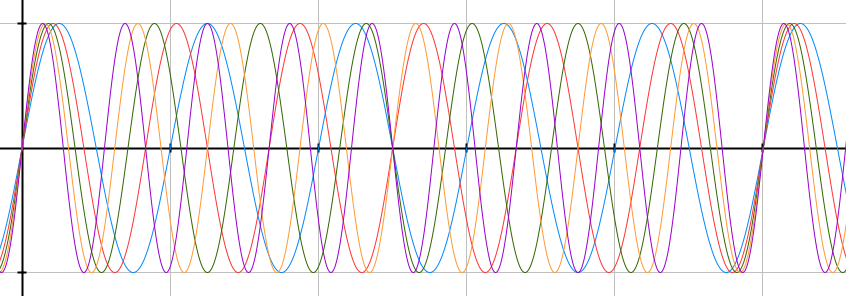
Concept animation of the five harmonic oscillators demonstrating the visual traveling waves, standing waves, beating and quasi chaos that they form across time.
Harmony and periodicity appears in many parts of the work with most important the harmonic oscillation of the balls. Additionally, the combining motion and the patterns that the five balls are producing along with way that the light fades in and out follows a sinusoidal form. The sound tones are simple sin waves that form a pentatonic scale, a scale that is consider as a very natural and harmonic.
The Sound of Pentavlos
In various significant points of the installation, for example when a ball passes from the middle of the motion path or when a tube is illuminated, the installation produces a tone. These tones are simple sinusoidal waves. All together they form a pentatonic scale with the following notes.

A pentatonic scale consists of five overtones and is derived directly from the natural physical phenomenon of the harmonic series. To maximize this effect, Pentavlos is using the Pythagorean tuning and not the equal temperament notes. To form the scale we use the following formulas:
| Pendulum | 1st | 2nd | 3rd | 4th | 5th | |
| Frequency Ratio | 1 | 9/8 | 81/64 | 3/2 | 27/16 | |
| Note | A | B | C# | E | F# | |
| Frequency (Hz) | Octave 2 | 110 | 123,8 | 139,2 | 165 | 185,6 |
| Octave 3 | 220 | 247,5 | 278,4 | 330 | 371,25 | |
| Octave 4 | 440 | 495 | 556,8 | 660 | 742,5 | |
Note: We are using the Pythagorean tuning and not the equal temperament notes.
The Technology of Pentavlos
The main parts of the installation are acrylic tubes, balls, leds and dc motors. Everything is controlled using an Arduino microcontroller. A custom android app installed on a phone is communicating via bluetooth with the Arduino and plays the sounds. The phone is also used to control various parameters of the installation (the power of the motors, the led luminosity e.c.t) .
 Screenshot of the android app that was developed
Screenshot of the android app that was developed
to play the sounds and control the installation.






