“Cellular Automaton Pi” is a visualization of an algorithm that uses a mathematical process called cellular automaton to generate random numbers and calculate the value of the mathematical constant Pi (π).

Pi is the ratio of a circle’s circumference to its diameter.
It cannot be defined as it has an infinite number of decimal digits.
It is approximately equal to 3.14159.
The algorithm uses Rule 30 of Wolfram cellular automaton, which generates patterns of the random triangles that are scrolling at the bottom of the screen.
 The visual pattern of rule 30 of Wolfram cellular automaton.
The visual pattern of rule 30 of Wolfram cellular automaton.
Rule 30 is an elementary cellular automaton introduced by Stephen Wolfram in 1983.
Using Wolfram’s classification scheme, Rule 30 is a Class III rule, displaying aperiodic, chaotic behavior.
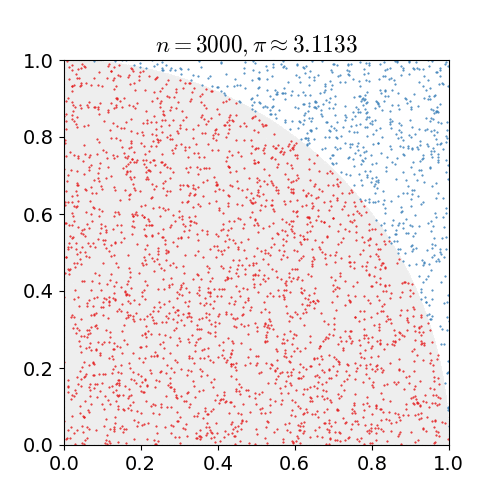
The algorithm recognizes the locations of triangles and by getting their horizontal position (which is almost random), calculates the value of Pi using the Monte Carlo method. The recognized triangles are marked with different colors. As it gets more random numbers, the value of calculated pi gets more accurate.
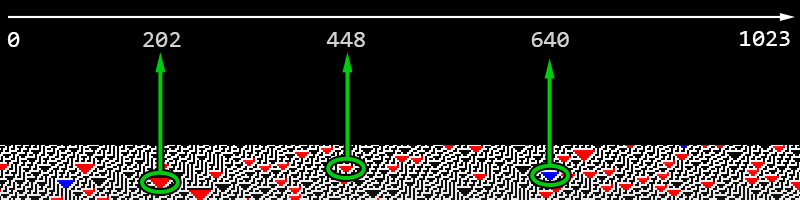 Example of 3 triangles located at positions 202, 448, and 640. The total width of Wolfram’s cellular automaton is 1024.
Example of 3 triangles located at positions 202, 448, and 640. The total width of Wolfram’s cellular automaton is 1024.
To calculate Pi(π) using the Monte Carlo method, we take pairs of random numbers as x and y and draw them on a 2D plane. Then we count the number of dots m that are within a distance of 1 from the origin, i.e. within the circle as shown below. The ratio (points within circle)/(total points) will be the approximate ratio of the area of the quarter circle to the area of the square which is π / 4.
\(\frac{quarter\ circle\ area}{square\ area}= \frac{\frac{pi*r^{2}}{4}}{r^{2}}=\frac{pi*r^{2}}{4 r^{2}}=\frac{pi}{4}\)